Μάθημα : Στοχαστικές Ανελίξεις
Κωδικός : MATH487
Περιγραφή Μαθήματος
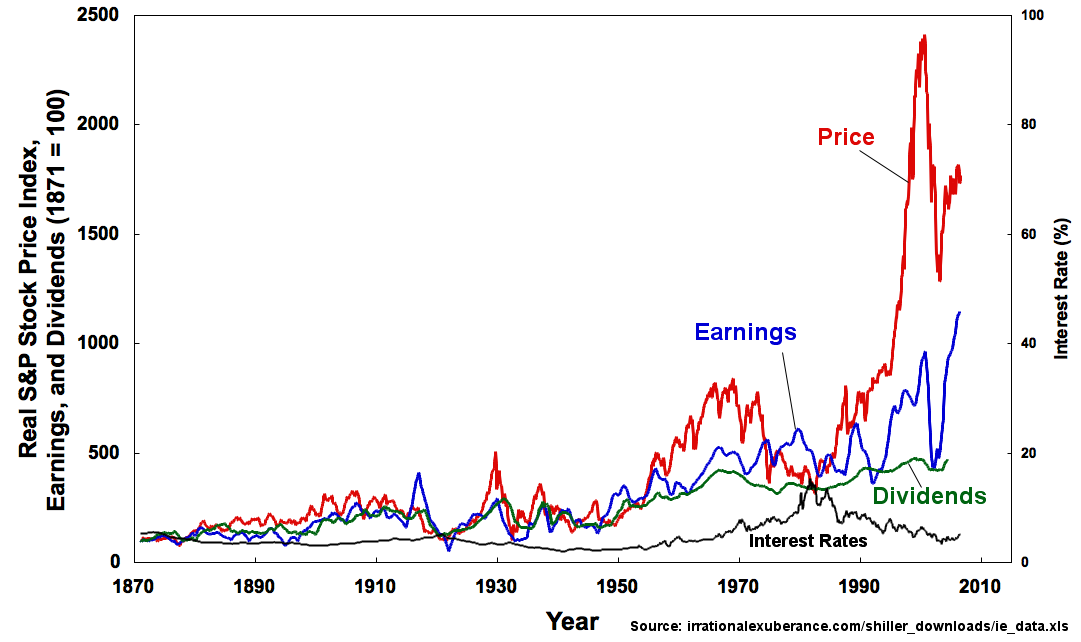
Στη θεωρία των πιθανοτήτων, μια στοχαστική διαδικασία, ή μερικές φορές μια τυχαία διαδικασία είναι μια συλλογή τυχαίων μεταβλητών, που αντιπροσωπεύουν την εξέλιξη κάποιου συστήματος με τυχαίες τιμές κατα τη πάροδο του χρόνου.
Αυτή είναι μια πιθανολογική ομόλογός σε μια ντετερμινιστική διαδικασία . Αντί να περιγράφει μια διαδικασία η οποία μπορεί να εξελιχθεί σε ένα μόνο τρόπο ( όπως στην περίπτωση, για παράδειγμα , λυσεων συνηθισμένων διαφορικων εξισωσεων ), σε μια στοχαστική ή τυχαία διαδικασία υπάρχει κάποια απροσδιοριστία : ακόμη και αν η αρχική κατάσταση (ή το σημείο εκκίνησης ) είναι γνωστό, υπάρχουν πολλές (συχνά απείρως πολλές ) κατευθύνσεις προς τις οποίες η διαδικασία μπορεί να εξελιχθεί .
Στην απλή περίπτωση του διακριτού χρόνου , σε αντίθεση με τη συνεχή φορά , μια στοχαστική διαδικασία περιλαμβάνει μια ακολουθία τυχαίων μεταβλητών και τις ακολουθιες των χρονων που σχετίζονται με αυτές τις τυχαίες μεταβλητές.
Σε αυτό το μάθημα θα ασχοληθούμε τόσο με Στοχαστικές Ανελίξεις Διακριτού χρόνου όσο και Στοχαστικές Ανελίξεις Συνεχούς χρόνου.
-
Περιεχόμενο μαθήματος
- Κατανομή Στοχαστικής Ανέλιξης. Παράμετροι στοχαστικής ανέλιξης. Στασιμότητα.
- Αλυσίδες Markov σε διακριτό χρόνο (ορισμοί, πιθανότητες μεταπηδήσεως ανωτέρας τάξεως, δικατάστατες αλυσίδες, κατάταξη των καταστάσεων, στάσιμη κατανομή).
- Αλυσίδες Markov σε συνεχή χρόνο (στοχαστική ανέλιξη Poisson, κατανομές ενδιάμεσων χρόνων και χρόνων αναμονής, στοχαστική ανέλιξη γεννήσεως-θανάτου, γραμμική ανέλιξη γεννήσεως-θανάτου, ανέλιξη των Furry-Yule, ανέλιξη θανάτου, εφαρμογές).
Διδάσκοντες
Απόστολος Μπουρνέτας
Θέση : Καθηγητής
Τομέας : Στατιστικής & Επιχειρησιακής Έρευνας
Ερευνητικά Ενδιαφέροντα : Επιχειρησιακή Έρευνα, Στοχαστικά Mοντέλα, Μαρκοβιανές Διαδικασίες Αποφάσεων, Βελτιστοποίηση Συστημάτων Εξυπηρέτησης, Μαθηματική Χρηματοοικονομική, Μαθηματική Ανάλυση Εφοδιαστικών Αλυσίδων.
e-mail :
Μέθοδοι διδασκαλίας
Διδασκαλία καθ΄ έδρας – Ασκήσεις
Ομάδα στόχος
Προπτυχιακοί Φοιτητές του Τμήματος Μαθηματικών του Καποδιστριακού Πανεπιστημίου Αθηνών.
Βοηθήματα
Ο. Χρυσαφίνου: Εισαγωγή στις Στοχαστικές Ανελίξεις
- Κατανομή Στοχαστικής Ανέλιξης. Παράμετροι στοχαστικής ανέλιξης. Στασιμότητα.
![aburnetas [ AT ] math.uoa.gr](http://noether.math.uoa.gr/Academia/statistiki/images/aburnetas)
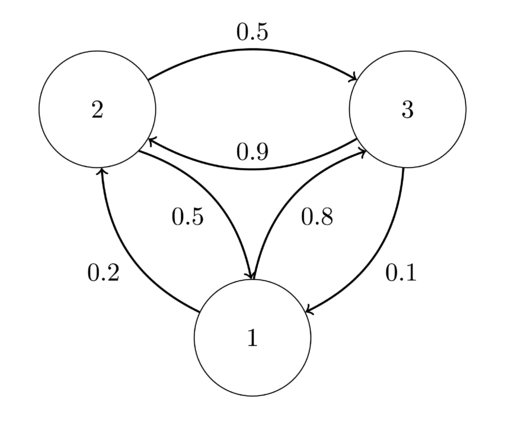Εισαγωγή στις στοχαστικές διαδικασίες, περιγραφή τους και εισαγωγή στην θεωρία μαρκοβιανών αλυσίδων διακριτού και συνεχούς χρόνου.
Λέξεις - Κλειδιά: Στοχαστική Ανέλιξη, Δυναμικά Συστήματα, Μεταβατική Κατανομή, Στάσιμες Στοχαστικές Ανελίξεις, Ανεξάρτητες Προσαυξήσεις, Ομογενείς προσαυξήσεις, Ανανεωτικές Διαδικασίες, Διάγραμμα Μεταβάσεων, Μαρκοβιανές Αλυσίδες, Μαρκοβιανή Ιδιότητα
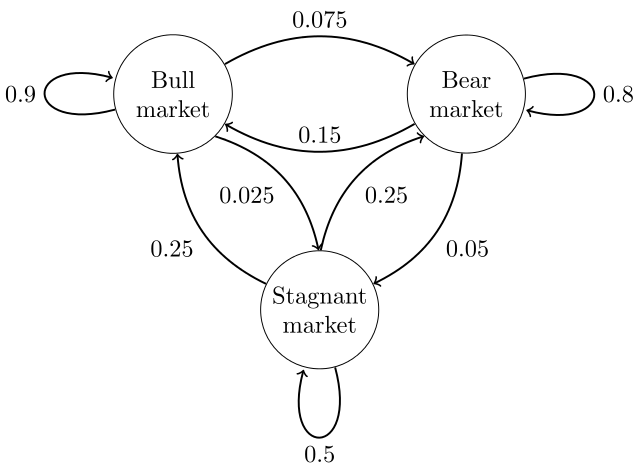Οι Μαρκοβιανές διαδικασίες αποτελούν κατάλληλα στοχαστικά μοντέλα για την περιγραφή και μελέτη στοχαστικών συστημάτων, η μελλοντική εξέλιξη των οποίων εξαρτάται αποκλειστικά από την παρούσα κατάστασή τους κάθε φορά, και όχι από τη συγκεκριμένη παρελθούσα ιστορία τους.
Οι Μαρκοβιανές διαδικασίες με διακριτό (πεπερασμένο ή αριθμήσιμο) χώρο καταστάσεων και διακριτό παραμετρικό χώρο.
Λέξεις - Κλειδιά: Μαρκοβιανή Αλυσίδα Διακριτού Χρόνου, Διακριτός Χρόνος, Μεταβατική Κατανομή, Ασυμπτωτική Συμπεριφορά, Ταξινόμηση Καταστάσεων, Χρόνος πρώτης Μετάβασης, Οριακή Κατανομή, Στοιχειώδες Ανανεωτικό Θεώρημα, επικοινωνία Καταστάσεων, Ανοικτή κλάση, Επαναληπτική κλάση, Κλειστή Κλάση, Οριακές Πιθανότητες, Αδιαχώριστη Αλυσίδα, Εξισώσεις Ισορροπίας,Διαχωρίσιμες Αλυσίδες, Πιθανότητες Απορρόφησης, Ανανεωμένη Χρόνοι Πρώτης Μετάβασης, Μαρκοβιανές Αλυσίδες για αμοιβές,
Στην ενότητα αυτή θα αναπτύξουμε τη γενική θεωρία των Μαρκοβιανών αλυσίδων συνεχούς χρόνου, δηλαδή των Μαρκοβιανών διαδικασιών με διακριτό χώρο καταστάσεων και συνεχή παραμετρικό χώρο.
Λέξεις - Κλειδιά: Μαρκοβιανές Αλυσίδες Συνεχούς Χρόνου, Αλυσίδα Συνεχούς χρόνου, Συνάρτηση πιθανότητας Μεταβάσεων, Chapman - Kolmogorov Equations, Προδρομικές Εξισώσεις, Αναδρομικές Εξισώσεις, Διαδικασία Poisson, Πίνακας Ρυθμών Μετάβασης, Ασυμπτωτική Συμπεριφορά, Αδιαχώριστες Μαρκοβιανές Αλυσίδες συνεχούς χρόνου, Εξισώσεις Ισορροπίας, Διαδικασία Γεννήσεων - Θανάτων, Εμφυτευμένη Μαρκοβιανή Αλυσίδα συνεχούν χρόνου
Ημερολόγιο
Ανακοινώσεις
Όλες...- - Δεν υπάρχουν ανακοινώσεις -