Μάθημα : Θεωρία Ομάδων και Εφαρμογές (E 2024-2025)
Κωδικός : PHYS299
Περιγραφή Μαθήματος
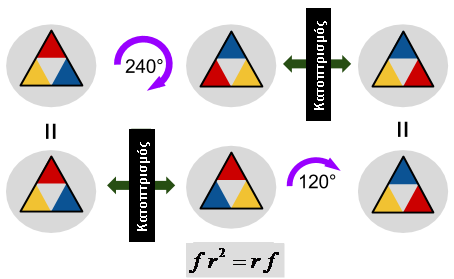
Η συμμετρία παίζει σημαντικό ρόλο στη μελέτη και τη βαθύτερη κατανόηση πολλών αρχών και φαινομένων της Φυσικής, ο δε ρόλος και οι συνέπειές της αναδεικνύονται με συστηματικό τρόπο μέσω της Θεωρίας Ομάδων. Το μάθημα «Θεωρία Ομάδων και Εφαρμογές» παρέχει στο/στη φοιτητή/φοιτήτρια την ευκαιρία να γνωρίσει και να κατανοήσει βασικές έννοιες και θεωρήματα της μαθηματικής Θεωρίας Ομάδων, καθώς και να εξοικειωθεί με τη χρήση τους στην επίλυση προβλημάτων που αφορούν στην επίπτωση της ύπαρξης συμμετριών στις ιδιότητες ενός κλασικού ή κβαντικού φυσικού συστήματος.
-
Διδάσκοντες
Φώτιος Διάκονος
Νικόλαος Στεφάνου
Μαθησιακοί στόχοι
Το μάθημα παρέχει στο/στη φοιτητή/φοιτήτρια την ευκαιρία να γνωρίσει και να κατανοήσει βασικές έννοιες και θεωρήματα της μαθηματικής Θεωρίας Ομάδων, καθώς και να εξοικειωθεί με τη χρήση τους στην επίλυση προβλημάτων που αφορούν στην επίπτωση της ύπαρξης συμμετριών στις ιδιότητες ενός φυσικού συστήματος. Με την επιτυχή παρακολούθηση και ολοκλήρωση του μαθήματος, ο φοιτητής θα είναι σε θέση:
- Να αντιλαμβάνεται την προέλευση νόμων διατήρησης στη Φυσική.
- Να κατανοεί σε βάθος τις ιδιότητες τελεστών και τη σύνδεση τους με θεμελιώδη μεγέθη της Κβαντικής Μηχανικής (στροφορμή, σπιν).
- Να χρησιμοποιεί τη Θεωρία Ομάδων για να προσδιορίζει βασικές ιδιότητες του ενεργειακού φάσματος (ιδιοτιμές, ιδιοκαταστάσεις) κβαντικών συστημάτων που έχουν συγκεκριμένες συμμετρίες.
- Να χρησιμοποιεί τη Θεωρία Ομάδων για να περιγράφει τους τρόπους ταλάντωσης μηχανικών συστημάτων σε συμμετρικές δομές.
- Να χρησιμοποιεί τη Θεωρία Ομάδων για να προσδιορίζει επιτρεπτές μεταβολές σε ένα φυσικό σύστημα που είναι αναλλοίωτο κάτω από ένα σύνολο μετασχηματισμών.
Με την επιτυχή παρακολούθηση και ολοκλήρωσή του, το μάθημα αποσκοπεί στο να έχει αποκτήσει ο/η φοιτητής/φοιτήτρια τις παρακάτω ικανότητες:
- Αναζήτηση, ανάλυση και σύνθεση δεδομένων και πληροφοριών, με τη χρήση και των απαραίτητων τεχνικών.
- Αυτόνομη εργασία.
- Αναλυτική και συνθετική σκέψη.
- Κριτική σκέψη.
- Επίλυση προβλημάτων.
Προτεινόμενα συγγράμματα
- Ι. Βέργαδος, Θεωρία Ομάδων, τόμοι Α’ και Β’, Εκδόσεις Ε. Καλαμαρά, 1991.
- S. Dresselhaus, Applications of Group Theory to the Physics of Solids, ΜΙΤ 2002.
- W. Byron and R.W. Fuller, Mathematics of Classical and Quantum Physics, Dover, 1992.
Μέθοδοι διδασκαλίας
ΤΡΟΠΟΣ ΠΑΡΑΔΟΣΗΣ: Πρόσωπο με πρόσωπο (σε έκτακτες περιστάσεις εξ αποστάσεως).
ΧΡΗΣΗ ΤΕΧΝΟΛΟΓΙΩΝ ΠΛΗΡΟΦΟΡΙΑΣ ΚΑΙ ΕΠΙΚΟΙΝΩΝΙΩΝ (ΤΠΕ): Ηλεκτρονική επικοινωνία με φοιτητές με χρήση ΤΠΕ. Υποστήριξη διδασκαλίας με χρήση Η/Υ, πλατφόρμα e-class.
ΟΡΓΑΝΩΣΗ ΔΙΔΑΣΚΑΛΙΑΣ: Διαλέξεις, ασκήσεις.
Μέθοδοι αξιολόγησης
Γραπτές τελικές εξετάσεις: 100%
Ημερολόγιο
Ανακοινώσεις
Όλες...-
Δευτέρα 16 Σεπτεμβρίου 2024 - 2:01 μ.μ.
-
Τετάρτη 28 Αυγούστου 2024 - 10:22 π.μ.
-
Παρασκευή 21 Ιουνίου 2024 - 1:48 μ.μ.